This is an old revision of the document!
Table of Contents
Optional Math of Waves
This is a brief survey of the math required to analyze waves at the first or second year university level.
Real numbers
If \$ (5) \times (5) = 25 \$ and \$ (-5) \times (-5) = 25 \$, what number (and it has to be the same number) can you put in the boxes so that:
\$$ \Box \times \Box = -25 \$$
It turns out that nowhere on the real number line is there a number such that when you multiply it by itself you get a negative number since two positive numbers give a positive number, and two negative numbers also give a positive number.
But could we invent one?
Complex Numbers
Let's create an imaginary number called \$ i \$ such that:
\$$ i = \sqrt{-1} \qquad \Rightarrow \qquad i^2 = -1 \$$
Even though \$ i \$ is nowhere on the real line (in math, we say that: \$ i \not\in \mathbb{R} \$), we can none-the-less perform interesting mathematical operations with it:
- We can add it to a real number and create a complex number:
\$$(1 + i) \$$
- We can multiply complex numbers together:
\begin{align*} (1+i)^2 &= 1 + 2i + i^2 \\ &= 1 + 2i - 1 \\ &= 2i \end{align*}
- We can find roots:
\begin{equation*} z^4 = 16 \Rightarrow z^2 = \left\{ \begin{array}{rl} 4 \Rightarrow z &= \pm 2 \\ -4 \Rightarrow z &= \pm 2i \end{array} \right. \end{equation*}
A Little Philosophy
If these weird numbers follow all of the algebra rules without inconsistencies, does it mean they exist as much as the real numbers? Aren't complex numbers a mere creation of mathematicians? Is mathematics discovered or invented?1)
In a certain way, negative numbers are just as weird as complex numbers: after all, we know what 5 cars look like, but −5 cars?
The Complex Plane
To represent a complex number graphically, we can use the horizontal axis for the real part and the vertical axis for the imaginary part. For example, \$ (1 + i) \$ could be represented as a point 45° up the horizontal axis and \$ \sqrt{2} \$ away from the origin.
You can move the point around to see what the polar representation \$ (r \angle \theta) \$ is.
Download polar.ggb
To convert between the Cartesian \$(a,b) \$ and the Polar \$ (r \angle \theta) \$ representations, only simple trigonometry and Pythagoras is needed.
| \$$ a + ib \rightarrow r\angle \theta \$$ | \$$ r\angle \theta \rightarrow a+ib \$$ |
|---|---|
| \$$ r^2 = a^2 + b^2 \$$ | \$$ a = r\cos\theta \$$ |
| \$$ \tan \theta = \dfrac{b}{a} \$$ | \$$ b = r\sin\theta \$$ |
Roots
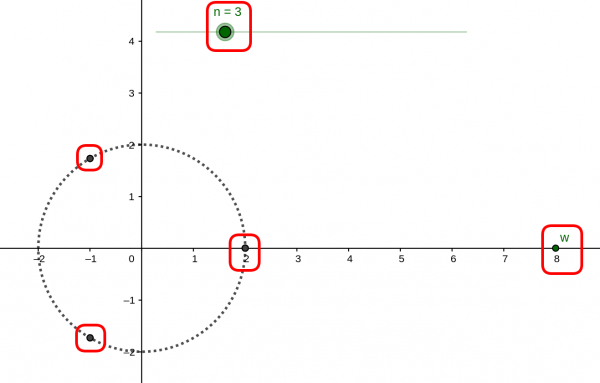
The complex plane allows us to take another look at how to find roots of the form \$ z^n = w \$. For example, if we set \$ w = 9 \$ and \$ n = 2 \$ on the graph below, we'll see that the roots to \$z^2 = 9 \$ are \$ z = \pm 3 \$.
Download complexroots.ggb
Without using the graph above, what do you expect the solution(s) to \$ z^3 = 8 \$ will be? That is, what number(s), when multiplied by itself three times gives 8?
Now move \$ w = 8 \$ and \$n = 3 \$ to have a look at the solutions.
The Euler Identity
The Euler identity exposes a deep relationship between trigonometric and exponential functions2):
\$$ e^{i \theta} = \cos \theta + i \sin \theta \$$
Let's use two different ways to verify that this mysterious identity works.
The Derivatives
If we separate this identity into two functions and take their derivatives, we notice that: \begin{align*} && f(\theta) &= e^{i \theta} &\text{ & }&& g(\theta) &= \cos \theta + i \sin \theta \\ \Rightarrow && f'(\theta) &= i e^{i \theta} &\text{ & }&& g'(\theta) &= -\sin \theta + i \cos \theta \\ \Rightarrow && f'(\theta) &= i \cdot f(\theta) &\text{ & }&& g'(\theta) &= i \cdot g(\theta) \end{align*}
We know that there's only one functions \$ h(x) \$ that satisfies the differential equation \$ h'(x) = ah(x) \$, and it is \$ h(x) = A e^{ax} \$ What Euler discovered is that when \$ a = i \$ , there's a second function that also satisfies the same differential equation! These two functions must therefore be one and the same.
Taylor
Another method to verify the Euler identity is to use Taylor series:
\begin{align*} e^x &= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \cdots \\ \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \\ \cos x &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \end{align*}
- Replace \$ x \$ with \$ i \theta \$ in the Taylor series of \$ e^x \$
- Replace \$ x \$ with \$ \theta \$ in the Taylor series for \$ \sin x \$ and \$ \cos x \$
- Add the Taylor series of \$ \cos \theta \$ and \$ i \sin \theta \$ together and you'll get the Taylor series for \$ e^{i \theta} \$
Exercises
- Use the Euler identity to get the following two useful results:
\$$ \cos \theta = \dfrac{e^{i \theta} + e^{-i \theta}}{2} \qquad \text { & } \qquad \sin \theta = \dfrac{e^{i \theta} - e^{-i \theta}}{2i} \$$
- Use the Euler identity to show that:
\$$ \cos (\theta + \phi) = \cos \theta \cos \phi + \sin \theta \sin \phi\\ \sin (\theta + \phi) = \cos \theta \sin \phi + \sin \theta \cos \phi \$$
- Use the two earlier results to show that:
\$$ \sin (\theta + \Delta \theta) + \sin (\theta - \Delta \theta) = 2 \cos \Delta \theta \sin \theta \$$
- Use the last result for \$ \sin(\theta + \phi) \$ but replace \$ \phi \$ with \$ \Delta \theta \$
\$$ \sin (\theta + \Delta \theta) = \cos \theta \sin \Delta \theta + \sin \theta \cos \Delta \theta \$$
Similarily, \begin{align*} && \sin (\theta - \Delta \theta) &= \cos \theta \sin(-\Delta \theta) + \sin \theta \cos (-\Delta \theta) \\ \Rightarrow && \sin (\theta - \Delta \theta) &= -\cos \theta \sin\Delta \theta + \sin \theta \cos \Delta \theta \\ \end{align*}
Adding both of these together, we get: \begin{align*} \sin (\theta + \Delta \theta) + \sin (\theta - \Delta \theta) &= \cos \theta \sin \Delta \theta + \sin \theta \cos \Delta \theta - \cos \theta \sin\Delta \theta + \sin \theta \cos \Delta \theta \\ &= 2\sin \theta \cos \Delta \theta \\ \end{align*}
Équations différentiels
Dans la physique des ondes, on aura bientôt à trouver la solutions d'une équation différentiel de ce type: \$$ a \ddot{x}(t) + b \dot{x}(t) + c x(t) = 0 \$$
Dans nos applications, les paramètres \$ a, b, c \$ serons tous des quantités réels et positive. Même sans avoir étudier le sujet d'équation différentiels en profondeurs, on peut imaginer qu'une solution possible serait \$ x(t)= e^{rt} \$ puisque la dérivé d'une fonction exponentiel est elle même une fonction exponentiel, ce qui est encourageant... L'étape suivante est donc d'essayer cette fonction dans l'équation différentiel, pour trouver les valeurs de \$ r \$ qui fonctionnent. Donc:
\$ \begin{align*} & x (t) = e^{rt} \\ \Rightarrow \qquad & \dot{x}(t) = r e^{rt} \\ \Rightarrow \qquad & \ddot{x}(t) = r^2 e^{rt} \end{align*} \$
et notre équation différentiel devient:
\$ \begin{align*} & a \ddot{x}(t) + b \dot{x}(t) + c x(t) = 0 \\ \Rightarrow \qquad & a (r^2 e^{rt}) + b (r e^{rt}) + c (e^{rt}) = 0 \\ \Rightarrow \qquad & e^{rt} (a r^2 + b r + c ) = 0 \\ \Rightarrow \qquad & a r^2 + b r + c = 0 \end{align*} \$
\$ \Rightarrow \qquad r = - \dfrac{b}{2a} \pm \dfrac{\sqrt{b^2 - 4ac}}{2a} \$
Puisque \$ r \$ contient une racine carré, il peut être réel, ou complexe. Pour simplifier la notation, disons que: \$ \alpha = \dfrac{b}{2a} \qquad \text{et} \qquad \beta = \dfrac{\sqrt{|{b^2 - 4ac}|}}{2a} \$
Nous pourrons donc dire que: \$ \begin{equation*} r = \left\{ \begin{array}{rl} -\alpha \pm \beta & \text{si } b^2 - 4ac > 0,\\ -\alpha \pm i \beta & \text{si } b^2 - 4ac < 0, \end{array} \right. \end{equation*} \$
Examinons les deux cas en plus de détails.
Cas 1:
Quand \$ b^2 - 4ac > 0 \$ , \$ r \$ est réel et la solutions général sera:
\$ \begin{align*} x(t) &= A_1 e^{r_1 t} + A_2 e^{r_2 t} \\ &= A_1 e^{( -\alpha + \beta) t} + A_2 e^{( -\alpha - \beta) t} \\ &= A_1 e^{-\alpha t} e^{\beta t} + A_2 e^{-\alpha t} e^{-\beta t} \end{align*} \$
\$$ x(t) = e^{-\alpha t} ( A_1 e^{\beta t} + A_2 e^{-\beta t} ) \$$
C'est normal d'avoir deux constantes d'intégrations puisque notre équation différentiel a une dérivé du second degré. Pour trouver ces constantes, ça nous prendrait des valeurs initiales.
Cas 2:
Quand \$ b^2 - 4ac < 0 \$ , \$ r \$ est complexe et nous utiliserons la formule de Euler pour simplifier notre solutions.
\$ \begin{align*} x(t) &= A_1 e^{r_1 t} + A_2 e^{r_2 t} \\ &= A_1 e^{( -\alpha + i \beta) t} + A_2 e^{( -\alpha - i \beta) t} \\ &= A_1 e^{-\alpha t} e^{i \beta t} + A_2 e^{-\alpha t} e^{-i \beta t} \\ &= e^{-\alpha t} ( A_1 e^{i \beta t} + A_2 e^{-i \beta t} ) \\ &= e^{-\alpha t} \Big( A_1 \big(cos( \beta t) + i \sin( \beta t) \big) + A_2 \big(cos( -\beta t) + i \sin( -\beta t) \big) \Big) \\ &= e^{-\alpha t} \Big( A_1 \big(cos(\beta t) + i \sin(\beta t) \big) + A_2 \big(\cos(\beta t) - i \sin(\beta t)\big)\Big) \\ &= e^{-\alpha t} \Big( (A_1 + A_2) \cos(\beta t) + i (A_1 - A_2) \sin(\beta t) \Big) \\ &= e^{-\alpha t} \Big( a_1 \cos(\beta t) + a_2 \sin(\beta t) \Big) \\ &= e^{-\alpha t} \Big( A \sin \phi \cos(\beta t) + A \cos \phi \sin(\beta t) \Big) \end{align*} \$
Dans les deux dernière ligne, nous avons ré-écrit les constantes d'intégration:
\$ \begin{align*} a_1 &= A_1 + A_2 & , a_2 &= i(A_1 - A_2) \\ a_1 &= A \sin \phi & , a_2 &= A \cos \phi \end{align*} \$
Pour finalement pouvoir utiliser une identité trigonométrique:
\$$ x(t) = A e^{-\alpha t} \sin(\beta t + \phi) \$$
Exemple
Nous avons donc deux types de solutions complètement différents qui dépendent de trois paramètres \$ a, b, c \$. Pour voir comment ces paramètres affectent le graphique, imaginons qu'une de nos conditions initiales est \$ \phi = \frac{\pi}{2} \$ . Ça veut dire que:
\$ \begin{align*} & a_1 = A \sin \pi/2 = A & & a_2 = A \cos \pi/2 = 0 \\ \Rightarrow \qquad & A_1 + A_2 = A & & A_1 - A_2 = 0 \\ \Rightarrow \qquad & A_1 = A/2 & & A_2 = A/2 \end{align*} \$
Dans ce cas particulier, nous avons donc:
\$ \begin{equation*} x(t) = \left\{ \begin{array}{rl} A e^{-\alpha t} \dfrac{e^{\beta t} + e^{-\beta t}}{2} & \text{si } b^2 - 4ac > 0 ,\\ A e^{-\alpha t} \cos(\beta t) & \text{si } b^2 - 4ac < 0 ,\\ \end{array} \right. \end{equation*} \$