This is an old revision of the document!
Table of Contents
Optional Math of Waves
This is a brief survey of the math required to analyze waves at the first or second year university level. If you did well in grade 12 high school math, you'll probably be able to follow this and learn some new and really cool math.
Real numbers
If \$ (5)^2 = 25 \$ and \$ (-5)^2 = 25 \$, what number can you put in the box so that:
\$$ \Box ^2 = -25 \$$
It turns out that there is no real number such that when you multiply it by itself you get a negative number, but could we invent an imaginary one?
Complex Numbers
Let's create an imaginary number called \$ i \$ such that:
\$$ i = \sqrt{-1} \qquad \Rightarrow \qquad i^2 = -1 \$$
Even though \$ i \$ is nowhere on the real line (in math, we say that: \$ i \not\in \mathbb{R} \$), we can none-the-less perform interesting mathematical operations with it:
- We can add it to a real number and create a complex number:
\$$(1 + i) \$$
- We can multiply complex numbers together:
\begin{align*} (1+i)^2 &= 1 + 2i + i^2 \\ &= 1 + 2i - 1 \\ &= 2i \end{align*}
- We can find roots:
\begin{equation*} z^4 = 16 \Rightarrow z^2 = \left\{ \begin{array}{rl} 4 \Rightarrow z &= \pm 2 \\ -4 \Rightarrow z &= \pm 2i \end{array} \right. \end{equation*}
A Little Philosophy
If these weird numbers follow all of the algebra rules without inconsistencies, does it mean they exist as much as the real numbers? Aren't complex numbers a mere creation by mad mathematicians? How about mathematics itself: is it discovered or invented?1)
In a certain way, negative numbers are just as weird as complex numbers: after all, we know what 5 cars look like, but what does −5 cars mean? And yet, in certain context (like temperature), we have no problem using negative numbers. Could it be that there are contexts where complex numbers make sense?
The Complex Plane
In the same way that we can represent real numbers by a point on the real number line...2):
... we can also represent a complex number graphically on a complex plane by using the horizontal axis for the real part and the vertical axis for the imaginary part. For example, \$ (1 + i) \$ would be represented as a point 45° up the horizontal axis and \$ \sqrt{2} \$ away from the origin:
Download polar.ggb
You can move the point around to look at other complex numbers on the plane.
To convert between the Cartesian \$(a,b) \$ and the Polar \$ (r \angle \theta) \$ representations, only simple trigonometry and Pythagoras is needed.
| \$$ a + ib \rightarrow r\angle \theta \$$ | \$$ r\angle \theta \rightarrow a+ib \$$ |
|---|---|
| \$$ r^2 = a^2 + b^2 \$$ | \$$ a = r\cos\theta \$$ |
| \$$ \tan \theta = \dfrac{b}{a} \$$ | \$$ b = r\sin\theta \$$ |
Note that very often, we use radians instead of degrees for the angle. There are a total 360° or 2π radians in a circle. While most people are used to degrees, a radian is actually much easier to picture:
- Imagine a circle.
- Now imagine the length from the centre to the circle (along the ——radius“).
- Take that length and lay it down on the perimeter of the circle.
- The angle that this length covers is 1 radian (because of the length of the radius on the circle).
- That's why a circle has 2π (because the circumference is 2πr)
Roots
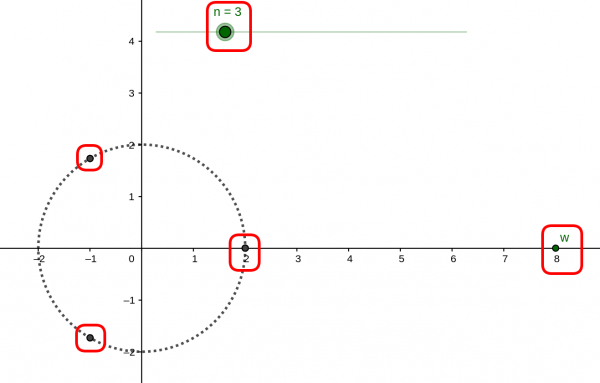
The complex plane has many useful applications, but one of them allows us to visualize roots of the form \$ z^n = w \$. For example, if we set \$ w = 9 \$ and \$ n = 2 \$ on the graph below, we'll see that the roots of \$z^2 = 9 \$ are \$ z = \pm 3 \$.
Download complexroots.ggb
Without using the graph above, what do you expect the solution(s) to \$ z^3 = 8 \$ will be? That is, what number(s), when multiplied by itself three times gives 8?
Now move \$ w = 8 \$ and \$n = 3 \$ to have a look at the solutions graphically, you might be surprised by what you find.
The Euler Identity
The Euler identity exposes a deep relationship between trigonometric and exponential functions3):
\$$ e^{i \theta} = \cos \theta + i \sin \theta \$$
Let's use two different ways to verify that this mysterious identity is true.
The Derivatives
If we separate this identity into two functions and take their derivatives, we notice that: \begin{align*} && f(\theta) &= e^{i \theta} &\text{ & }&& g(\theta) &= \cos \theta + i \sin \theta \\ \Rightarrow && f'(\theta) &= i e^{i \theta} &\text{ & }&& g'(\theta) &= -\sin \theta + i \cos \theta \\ \Rightarrow && f'(\theta) &= i \cdot f(\theta) &\text{ & }&& g'(\theta) &= i \cdot g(\theta) \end{align*}
We know that there's only one functions \$ h(x) \$ that satisfies the differential equation \$ h'(x) = ah(x) \$, and it is \$ h(x) = A e^{ax} \$ What Euler discovered is that when \$ a = i \$ , there's a second function that also satisfies the same differential equation! These two functions must therefore be one and the same.
Taylor
Another method to verify the Euler identity is to use Taylor series:
\begin{align*} e^x &= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \cdots \\ \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \\ \cos x &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \end{align*}
- Replace \$ x \$ with \$ i \theta \$ in the Taylor series of \$ e^x \$
- Replace \$ x \$ with \$ \theta \$ in the Taylor series for \$ \sin x \$ and \$ \cos x \$
- Add the Taylor series of \$ \cos \theta \$ and \$ i \sin \theta \$ together and you'll get the Taylor series for \$ e^{i \theta} \$
Euler Identity and Polar-Cartesian Representations
In the previous section, we saw that a complex number \$z = a + ib \$ could be represented as a point \$(a, b)\$ on the complex plane, which could also be viewed in polar coordinates as \$r\angle \theta \$. We saw that to convert between the Cartesian \$(a,b) \$ and the Polar \$ (r \angle \theta) \$ representations, only simple trigonometry and Pythagoras is needed:
| \$$ a + ib \rightarrow r\angle \theta \$$ | \$$ r\angle \theta \rightarrow a+ib \$$ |
|---|---|
| \$$ r^2 = a^2 + b^2 \$$ | \$$ a = r\cos\theta \$$ |
| \$$ \tan \theta = \dfrac{b}{a} \$$ | \$$ b = r\sin\theta \$$ |
This means that:
\begin{align*} z &= a + ib \\ &= r\cos\theta + i r\sin\theta \\ &= r\big( \cos\theta + i \sin\theta \big) \\ &= r e^{i\theta} \end{align*}
This offers another interpretation of the Euler identity as the algebraic conversion between Cartesian and Polar coordinates:
| Cartesian | Polar | |
|---|---|---|
| Graphical | \$$(a, b) \$$ | \$$ (r\angle \theta) \$$ |
| Algebraic | \$$z = a + ib\$$ | \$$ z = re^{i\theta} \$$ |
This now allows us to simplify a lot of difficult mathematics. For example let's look at the root problem \$z^3 = 8 \$. Since the number 8 on the complex plane is the point \$(8,0)\$, in polar coordinates, it can be any of the following: \$8\angle 0, 8\angle 2\pi, 8\angle 4\pi, \cdots \$ This is because we can go around the circle as many times as we want and return to the same point. Since we expect three roots, let's use the first three polar representations of 8:
\$$ z^3 = 8 = \left\{ \begin{array}{c} 8e^{0 i} \\ 8e^{2\pi i} \\ 8e^{4\pi i}\\ \vdots \end{array} \right. \$$
\$$ \Rightarrow z = \left\{ \begin{array}{lcl} \left(8e^{0 i}\right)^{\frac{1}{3}} &=& 8^{\frac{1}{3}} e^{\frac{0}{3}} = 2\\ \left(8e^{2\pi i}\right)^{\frac{1}{3}} &=& 8^{\frac{1}{3}} e^{\frac{2\pi}{3}i} = 2 \left(\cos \frac{2\pi}{3} + i \sin \frac{2\pi}{3}\right) = 2 \left(-\frac{1}{2} + i \frac{\sqrt{3}}{2}\right) = -1 + i\sqrt{3} \\ \left(8e^{4\pi i}\right)^{\frac{1}{3}} &=& 8^{\frac{1}{3}} e^{\frac{4\pi}{3}i} = 2 \left(\cos \frac{4\pi}{3} + i \sin \frac{4\pi}{3}\right) = 2 \left(-\frac{1}{2} - i \frac{\sqrt{3}}{2}\right) = -1 - i\sqrt{3} \\ &\vdots& \end{array} \right. \$$
If we had used more than 3 numbers, the roots would have started repeating. If we had used less than 3, we would have missed some answers in the same way that there are two answers to \$z^2 = 9 \$ (namely \$z = \pm 3 \$).
Cartesian vs Polar
Which is the best representation: Cartesian, \$z = a + i b \$, or Polar, \$z = re^{i\theta}\$. As you might expect, it depends on what you're trying to do... For example, let's take:
\$$z_1 = 1 + i = \sqrt{2}e^\left(i\frac{\pi}{4}\right) \quad \text{and} \quad z_2 = -1 + i = \sqrt{2}e^\left(i\frac{3\pi}{4}\right) \$$
Imagine having to add, subtract, multiply, divide or divide these together. Or raise them to a power, or take a root of them. Which of the two representations do you think would be easiest to use for each operation?
The lesson here is that since the polar representation uses exponents, and exponents turn multiplication into addition4), the polar representation is easiest for multiplication, division, exponentiation, and roots. It's essentially why the dB scale is so useful.
Important Algebraic Results
- Use the Euler identity to get the following two useful results:
\$$ \cos \theta = \dfrac{e^{i \theta} + e^{-i \theta}}{2} \qquad \text { & } \qquad \sin \theta = \dfrac{e^{i \theta} - e^{-i \theta}}{2i} \$$
- Use the Euler identity to show that:
\$$ \cos (\theta + \phi) = \cos \theta \cos \phi + \sin \theta \sin \phi\\ \sin (\theta + \phi) = \cos \theta \sin \phi + \sin \theta \cos \phi \$$
- Use the two earlier results to show that:
\$$ \sin (\theta + \Delta \theta) + \sin (\theta - \Delta \theta) = 2 \cos \Delta \theta \sin \theta \$$
This last result is the basis behind why modulating the amplitude of a carrier produces side bands.
\$$ e^{i \pi} = \cos (\pi) + i \sin (\pi) = -1 + 0i = -1\$$ \$$ \Rightarrow e^{i \pi} = -1\$$ which is amazingly beautiful because it relates \$ e = 2.71828... \$, \$i = \sqrt{-1} \$, \$\pi = 3.14159... \$, and \$-1\$ in the most surprising and elegant way.