Table of Contents
COVID-19 Spread (Part I)
- I'm not an epidemiologist, doctor, or any kind of expert on the subject. I just look at the numbers.
- The original post was written on March 16. Since then, I've updated the graphs with daily numbers, and added another section at the end.
One of the key messages from today's PM announcement is that things will get worse before they get better. I wanted to have a sense of the rate at which COVID-19 is spreading in Canada, so I made a graph, and did some math.1)
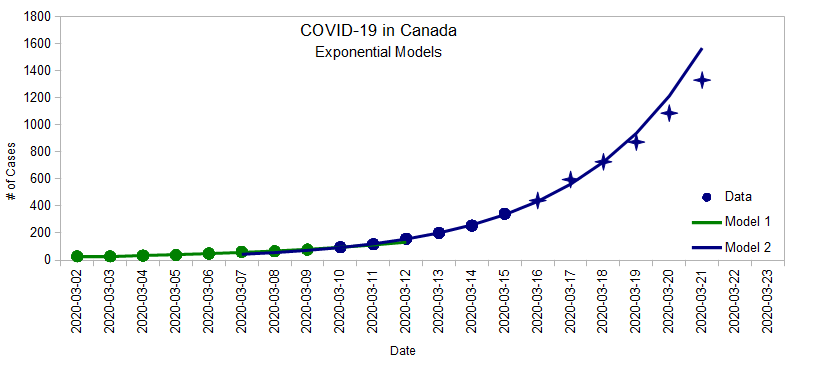
First, I got the data from https://www.covid-19canada.com, plotted them on a graph, and tried to use a basic exponential model to extract some key information.
| Date | Count | Date | Count | Date | Count | ||
|---|---|---|---|---|---|---|---|
| 2020-03-01 | ? | 2020-03-08 | 64 | 2020-03-15 | 342 | ||
| 2020-03-02 | 27 | 2020-03-09 | 77 | 2020-03-16 | 441† | ||
| 2020-03-03 | 27 | 2020-03-10 | 95 | 2020-03-17 | 596† | ||
| 2020-03-04 | 33 | 2020-03-11 | 117 | 2020-03-18 | 727† | ||
| 2020-03-05 | 37 | 2020-03-12 | 157 | 2020-03-19 | 873† | ||
| 2020-03-06 | 48 | 2020-03-13 | 201 | 2020-03-20 | 1087† | ||
| 2020-03-07 | 60 | 2020-03-14 | 254 | 2020-03-21 | 1331† |
† Data from March 16 onward has been added to the original model without modifications.
There seems to be two different patterns in this two-week period:
- Between March 2 and March 10 (ish) (green line), the number of cases was doubling every 4.1 days.
- But since March 10 (ish) (blue line), the number of cases has been doubling every 2.7 days.
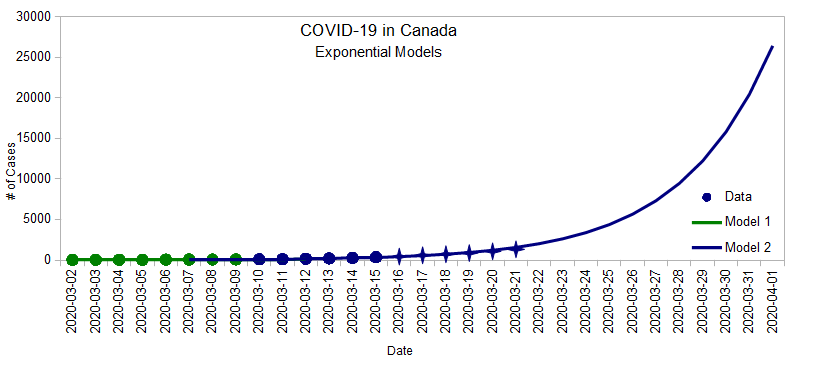
If the blue exponential pattern continues:
- We should have close to 1600 cases by the end of Saturday (from 342 on Sunday)
- A week after that: over 9000 cases
- By the end of April 1: 26,000 cases (similar to Italy today)
So there's a very real sense in which, if we don't do anything different, we could simply be about 15 days behind Italy...
But doing the right things can change that future. In reality, the spread of the infection follows more of a Logistic Function. At the beginning, it looks like an exponential, but then it flattens out. This is what the news keeps referring to when they say that social distancing and proper hand washing can help “flattening the curve” more quickly.
 The real question is how soon we will reach that middle point, and at what height.
The real question is how soon we will reach that middle point, and at what height.
Here's a good video that explains this sort of math and why being able to think in exponential term is important for non-linear systems such as this one.
And here's another one with different animations that complements it very nicely.
Here's an interesting article from The Washington Post showing basic random simulations for four different cases (free-for-all, attempted quarantine, mild moderate distancing, extensive social distancing).

More on the Logistic Function
This is an update from March 19th.
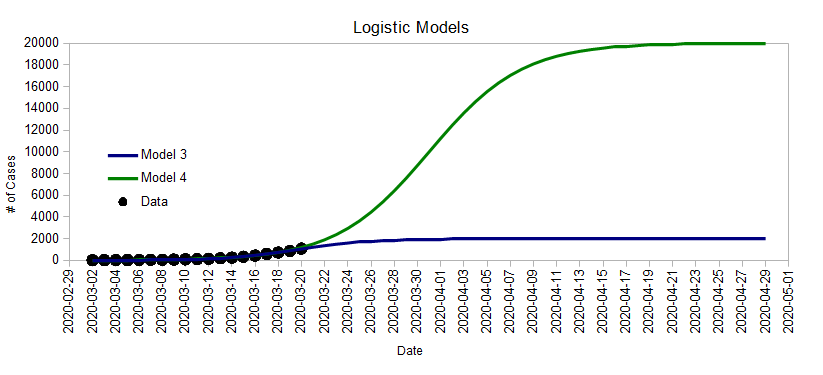
This section illustrates how eventhough the infection follows a Logistic Function, that fact alone doesn't necessarily help us predict the future. For example, here are two very different models that fit the current data pretty well:
The equation for “Model 3” is:
\$$N = \frac{2000}{1 + e^{-0.32(t - 21.1)}}\$$
It reaches its halfway point around March 21 and peaks at 2000 people infected. Unfortunately, “Model 4” also fits the data just as well:
Its equation is:
\$$N = \frac{20000}{1 + e^{-0.24(t - 32)}}\$$
But it reaches its halfway point at on April 1st and peaks at 20,000 people.
Reality could be anywhere in between, or even higher ‒ I could have easily created a curve that fits the current data just as well and peaks at 2 million people. The point is that we just don't know because it all depends on how we act now.
Part II
This page is no longer being updated. Have a look at Part II for more updates.